|
���w������
�ŗD�G��
|
����n���o�[�K�[�X�ɂ́A�P�O�O�~�̃n���o�[�K�[�A�P�T�O�~�̃`�[�Y�o�[�K�[�A�Q�T�O�~�̂Ă�₫�o�[�K�[������B������̔���グ�ׂ�ƕ\�T�̂悤�ɂȂ����B�܂��A����Ƃ��̐l���ׂ�ƕ\�U�̂悤�ɂȂ����B������ނ̃n���o�[�K�[���Q�ȏ㔃�������q�����Ȃ��Ƃ��āA�R�T�O�~�A�S�O�O�~�����l�����A���ꂼ�ꋁ�߂�B
�\�T
|
�n���o�[�K�[�̎��
|
�n���o�[�K�[
|
�`�[�Y�o�[�K�[
|
�Ă�₫�o�[�K�[
|
|
���ꂽ���i�j
|
�Q�W
|
�S�O
|
�R�P
|
�\�U
|
����i�~�j
|
�P�O�O
|
�P�T�O
|
�Q�O�O
|
�Q�T�O
|
�R�O�O
|
�S�O�O
|
|
�l���i�l�j
|
�V
|
�P�U
|
�R�O
|
|
|
�T
|
�i�����j�R�T�O�~���R�l�A�S�O�O�~���U�l
|
����i�u�]��
�n���o�[�K�[�X�ŁA�������������q����̐l�������߂�Ƃ������ł���A���퐶���ɖ���������ʂŘA�������������p���Ă���B���������m�ɐݒ肳��Ă���A���J�ɖ��Â��肪����Ă���B��@�ł́A���C���ȊO�ɂR�ڂ̕�����p���āA�R���̘A���������𗧂āA�����悭�����Ă���_���]���ł���B�@�@�@
�@�D�G��
|
�A�}�`���A�̖싅���s���邱�ƂɂȂ�A���`�[���W�܂����B�i���͋����Ƃ���j�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�܂����`�[�������[�O��i���̃`�[���ƂP�������키�j�ɂ���Ĕ����Ɍ��炵�A�������g�[�i�����g��i�����c���j�ɂ���Đ�킹��B���[�O��A�g�[�i�����g��A���킹�ĉ������s���邩�B
�i�����j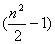 ���� ����
|
����i�u�]��
�X�|�[�c�̑��ɂ悭�p�����郊�[�O������A�g�[�i�����g��������ނɂ����A���퐶���ɖ����������ł���B���ꂼ��̎��������̐����𐔊w�I�ɂƂ炦�A��������ŕ\���A�������悤�Ƃ����_���]���ł���B
|
�C�X���U�A���ɕ���ł��āA���ꂼ��ԍ������܂��Ă���B�܂��A�P�`�U�܂ł̐������L�������J�[�h������B���̃J�[�h���悭�����āA�܂��`���P�������A�����Ăa���P�������āA���̃J�[�h�̐����Ɠ����ԍ��̃C�X�ɍ��邱�Ƃɂ���B���̎��A�`����Ƃa���ƂȂ�ɍ���m�������߂Ȃ����B�܂��A�C�X�̕��ѕ����ς�����Ƃ��A�`����Ƃa���ׂɍ���m���͂ǂ��Ȃ�ł��傤�B
�i�����j �ǂ����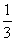
|
����i�u�]��
�����������ĐȂ����߂�Ƃ����A���퐶���ł悭�����ʂ���ɂ��Ă���_���悢�B�`����Ƃa���ׂɍ���ꍇ�̐�����̓I�ɐ����Ă݂�ƁA���̊m���͂����̕��ѕ��ɊW�Ȃ������ł��邱�Ƃ�������A��ςȋ�����������B
�����
|
�`�N�̒a�����̂��Ƃł��B�P�[�L�ɂ낤�����𗧂Ă悤�Ƃ����Ƃ���A���a�P�T�����̃P�[�L�ɉ~��ɂQ��ɗ��Ă悤�Ƃ������ƂɂȂ�܂����B�����đ傫���~���������~���T�{�������Ă邱�Ƃɂ��܂����B�낤�������m�̊Ԋu�͂��ׂē����ł��B�������A�~�̒��S���珬�����~�͔��a�T�����A�傫���~�͔��a�P�O�����Ƃ��܂��B�`�N�͉��ł��傤�B
�@�@�@ �i�����j�P�T��
|
����i�u�]��
�P�[�L�ɂ낤�����𗧂Ă�Ƃ����o�����ނɂ����A���퐶���ɖ����������ł���B���Ԋu�ɂ낤�����𗧂Ă�Ƃ����ݒ肩��o��҂��~�`�̃P�[�L�̒��ɐ}�`�I�Ȕ�������Nj����悤�Ƃ����ӎ����`����Ă��āA�f���炵���B
|
������A�`����Ƃa����͂S�O�O�~�������āA�u���������v�ɍs���܂����B�`����͂P��P�O�O�~�̂����A�a����͂P��Q�O�O�~�̂����ɂł��邾�����킵�܂����B�\�莆�ɂ͂����A�����Ă����������ł��B
�i�\�莆�r
�P��P�O�O�~
�P��Q�O�O�~
|
���܁@�@�@�P�{
�a�܁@�@�@�R�{
�b�܁@�@�@�T�{
�c�܁@�@�P�O�{
�c�O�܁@�Q�P�{
|
�u���������v �R�[�i�[
�i���Ȃ��j
|
���܁@�@�@�S�{
�a�܁@�@�@�U�{
�b�܁@�@�@�W�{
�c�܁@�@�P�O�{
�c�O�܁@�P�Q�{
|
���܂�������m���������̂́A�`���a����A�ǂ���ł��傤�B�@�@�@
�i�����j �a����
|
����i�u�]��
�g�߂Ȃ��������̏�ʂŁA�m���Ɗ֘A���������w���炵�����ƂȂ��Ă���B�F�X�ȏ܂����邪�A�����̒l�i�Ɠ��܂̐��A�y�т����̍��v���ɒ��ڂ���Ɩ��������ł���悤�ɂȂ��Ă���B
|
�s�ō���Ă���n��̐V�����Q�U�Z�̊w�Z���w�ǂ��Ă���B�����Ŗ����w�ǂ��Ă���w�Z����A�V����Q�S�O�~�Ƒ�����������Ă���B�����͂R�O���������͂U�O�~�A�R�O�����ȏ�͂W�O�~�œ͂��Ă���B�������A���̓��̉��Z���͒��ړn���Ă���̂ŁA�����͂�����Ȃ��B���ړn���Ă���w�Z�̐��́A�����U�O�~�Ŕz�B���Ă���w�Z���Ɠ����ł���B�����͐V����Ƒ������킹�ĂV�C�U�Q�O�~��������B���̂Ƃ��A�����W�O�~�Ŕz�B����Ă���w�Z�́A���Z�ł��傤�B�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@ �i�����j�P�Q�Z
|
����i�u�]��
�V�����w�ǂ��Ă���w�Z������Ƃ����ݒ������A�w�Ǘ����l������ł���B�V����̑��ɑ������l���Ă����ہA�����Ƃ����v�f�������ꂽ�_���f���炵���B
|